What Is X 9 18 2x
New Snow
May 10, 2025 · 5 min read
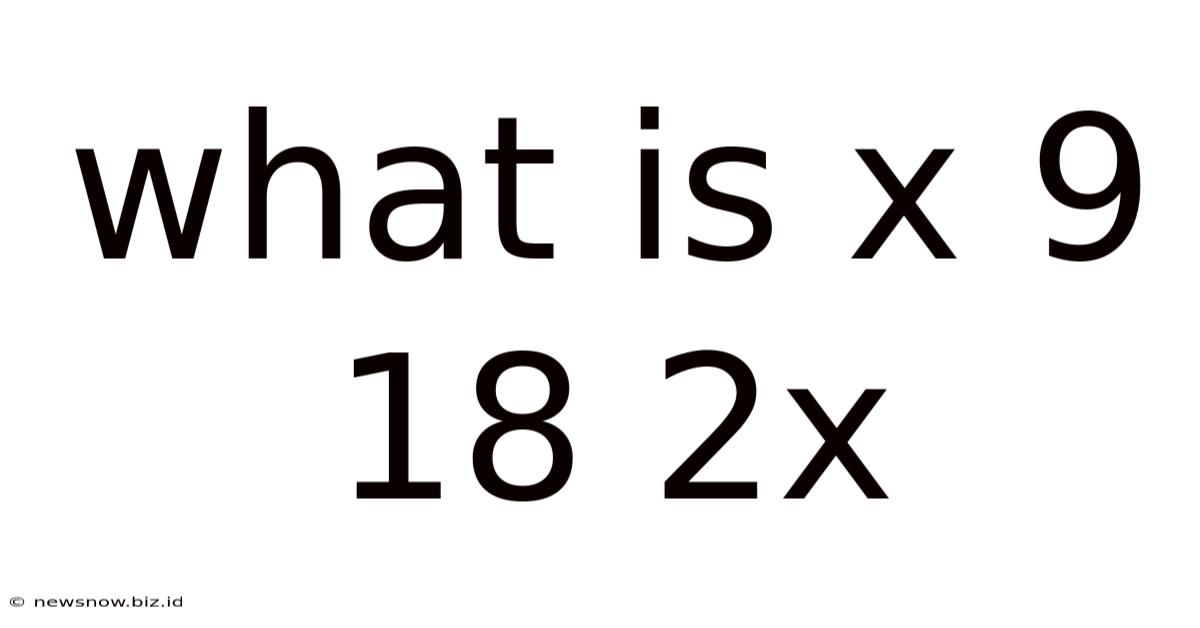
Table of Contents
What is x: 9, 18, 2x? Unraveling the Mystery of Mathematical Sequences
This seemingly simple question, "What is x: 9, 18, 2x?", hides a fascinating exploration into the world of mathematical sequences and problem-solving. At first glance, it appears straightforward, but delving deeper reveals the nuances of pattern recognition, algebraic manipulation, and the importance of understanding underlying mathematical principles. This article will comprehensively unpack this puzzle, exploring different approaches to solving it, and highlighting the broader mathematical concepts it embodies.
Understanding the Nature of the Sequence
The sequence 9, 18, 2x presents a challenge because it's incomplete. To find the value of x, we need to identify the underlying pattern or rule governing the relationship between the numbers. There are several possible approaches, each requiring a different line of reasoning.
1. Identifying Arithmetic Progressions
One common approach is to look for an arithmetic progression. An arithmetic progression is a sequence where the difference between consecutive terms remains constant. Let's examine the given sequence:
- Difference between the first two terms: 18 - 9 = 9
- Potential difference between the second and third terms: 2x - 18
If this is an arithmetic progression, then the difference between consecutive terms must be consistent. Therefore, we can set up an equation:
2x - 18 = 9
Solving for x:
2x = 27 x = 13.5
This solution suggests that the sequence is 9, 18, 27. The common difference is 9. This is a valid solution, but it's important to remember that other solutions may exist.
2. Exploring Geometric Progressions
Another possibility is a geometric progression. A geometric progression is a sequence where each term is the product of the previous term and a constant ratio. Let's investigate:
- Ratio between the first two terms: 18 / 9 = 2
If it's a geometric progression, the ratio between the second and third terms should also be 2. Therefore:
2x / 18 = 2
Solving for x:
2x = 36 x = 18
This solution implies the sequence is 9, 18, 36. The common ratio is 2. This is another valid solution.
3. Considering Other Mathematical Relationships
Beyond arithmetic and geometric progressions, there could be other, more complex relationships at play. For example, the sequence might follow a polynomial pattern, a Fibonacci-like sequence, or some other defined rule. The absence of additional terms makes it challenging to definitively determine the pattern without further information.
The Importance of Context and Additional Information
The key takeaway from this analysis is the critical role of context. Without additional information about the sequence, multiple solutions are possible. The problem highlights the importance of providing sufficient data to uniquely determine a mathematical relationship. For instance, if we were told the sequence represents the growth of a specific organism, a pattern might become more apparent, lending itself to a specific type of progression.
Expanding the Problem: Adding More Terms and Context
Let's explore how adding more terms to the sequence would influence our solution. Suppose the sequence continued as: 9, 18, 2x, y. With an additional term, we increase the constraints, potentially reducing the number of valid solutions. Identifying patterns would become much easier. For example:
- If the sequence were 9, 18, 27, 36, it's clearly an arithmetic progression with a common difference of 9.
- If the sequence were 9, 18, 36, 72, it's equally clear that it's a geometric progression with a common ratio of 2.
The more terms we have, the more accurately we can define the underlying pattern.
Applications of Sequence Analysis in Real-World Problems
Understanding sequences and patterns is not merely an academic exercise. It finds extensive application in various real-world scenarios:
- Financial Modeling: Predicting stock prices, analyzing investment growth, and understanding economic trends often involve identifying patterns in time-series data, which are essentially sequences of numerical values.
- Data Science and Machine Learning: Sequence analysis is a fundamental component of machine learning algorithms used in applications ranging from natural language processing (analyzing text sequences) to genetic sequencing (analyzing DNA sequences).
- Signal Processing: Analyzing signals, such as audio or video data, often involves identifying patterns and trends in the sequence of signal values.
- Physics and Engineering: Many physical phenomena, such as wave propagation or the motion of objects, can be modeled using sequences and mathematical patterns.
- Computer Science: Algorithms and data structures often rely on the principles of sequence analysis for efficient processing and manipulation of information.
Beyond the Numbers: Developing Problem-Solving Skills
The puzzle "What is x: 9, 18, 2x?" serves as more than just a mathematical exercise; it's a valuable tool for developing critical problem-solving skills. Here's how:
- Pattern Recognition: The ability to identify patterns and relationships is crucial in problem-solving across many disciplines. This problem encourages the development of this essential skill.
- Logical Reasoning: Determining the value of x requires applying logical reasoning to deduce the underlying rule governing the sequence.
- Algebraic Manipulation: Solving for x involves applying algebraic principles, reinforcing fundamental mathematical concepts.
- Critical Thinking: Understanding the limitations of incomplete data and the multiple possible solutions encourages critical thinking about the nature of the problem and the reliability of conclusions.
- Creativity and Exploration: Instead of solely focusing on conventional arithmetic or geometric progressions, one can explore other mathematical functions or relationships, stimulating creativity and a more holistic approach to problem-solving.
Conclusion: The Enduring Power of Mathematical Inquiry
The seemingly simple question "What is x: 9, 18, 2x?" provides a rich and engaging exploration into the world of mathematical sequences, problem-solving techniques, and the broader implications of pattern recognition. While multiple solutions are possible with the limited information provided, the process of analyzing the sequence enhances our understanding of mathematical concepts and cultivates valuable problem-solving skills applicable far beyond the confines of this specific puzzle. The challenge highlights the importance of context, the power of critical thinking, and the enduring beauty of mathematical inquiry. It encourages us to move beyond finding simple answers and to appreciate the elegance and complexity embedded within even the most straightforward mathematical problems. The true value lies not just in the solution but in the journey of discovery itself.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is X 9 18 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.