7 Is Ten Times The Value Of What Number
New Snow
May 10, 2025 · 5 min read
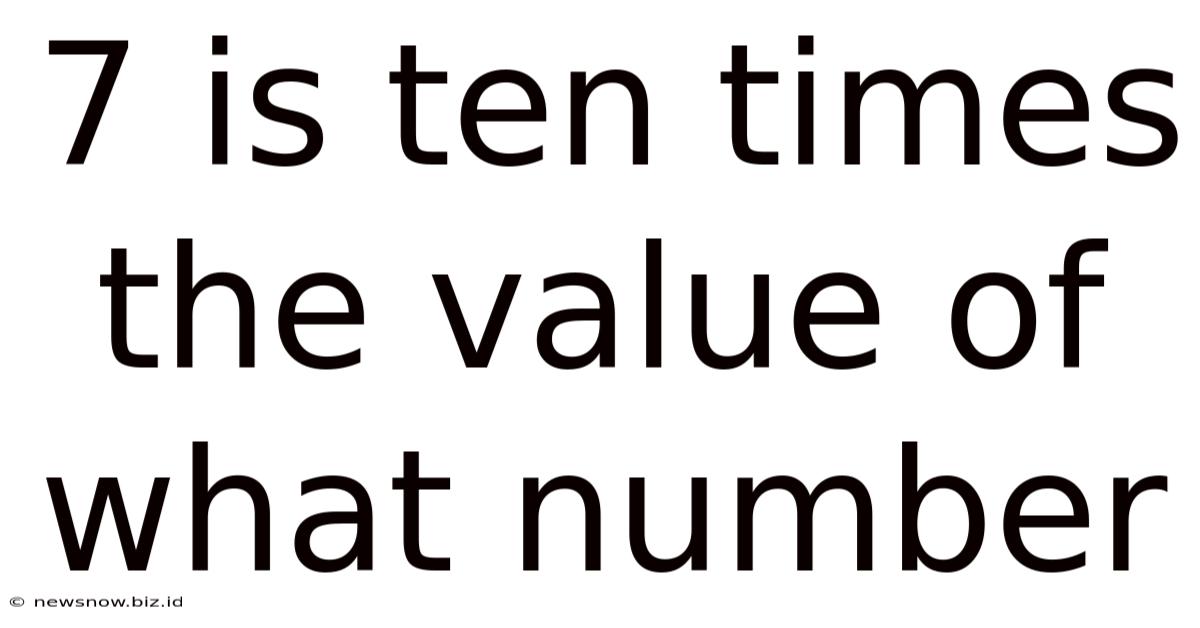
Table of Contents
7 is Ten Times the Value of What Number? Unlocking the Power of Decimals
This seemingly simple question, "7 is ten times the value of what number?", opens a door to a fundamental concept in mathematics: decimal numbers. Understanding this concept is crucial, not just for passing math tests, but for navigating everyday life, from calculating tips to understanding financial reports. This article will delve deep into the solution, exploring the underlying mathematical principles and demonstrating various approaches to solving similar problems. We'll also explore the broader context of decimal numbers and their significance.
Understanding the Problem: Deciphering the Language of Math
The question "7 is ten times the value of what number?" presents a word problem that needs to be translated into a mathematical equation. Let's break down the language:
- "7 is": This translates to "7 =". The equals sign signifies equivalence.
- "ten times the value of": This indicates multiplication by 10.
- "what number": This is our unknown variable, which we can represent with 'x'.
Therefore, the complete mathematical equation becomes: 7 = 10x
Solving the Equation: Finding the Unknown
Now that we have a clear equation, we can solve for 'x', the unknown number. To isolate 'x', we need to perform the inverse operation of multiplication, which is division. We divide both sides of the equation by 10:
7 / 10 = 10x / 10
This simplifies to:
x = 0.7
Therefore, 7 is ten times the value of 0.7.
Different Approaches to Solving the Problem
While the above method is straightforward, there are other ways to approach this problem, reinforcing the understanding of the underlying mathematical principles:
1. Using Proportions: A Visual Approach
Proportions offer a visual way to grasp the relationship between the numbers. We can set up a proportion as follows:
10 / 1 = 7 / x
Cross-multiplying gives us:
10x = 7
Dividing both sides by 10, we again arrive at:
x = 0.7
This method highlights the proportional relationship between the numbers, providing a different perspective on the problem.
2. Thinking in Reverse: The Inverse Operation
Instead of directly solving the equation, we can think about the problem in reverse. If 7 is ten times a number, then that number must be one-tenth of 7. One-tenth is the same as dividing by 10:
7 / 10 = 0.7
This approach demonstrates a deeper understanding of the inverse relationship between multiplication and division.
Understanding Decimal Numbers: Beyond the Solution
The solution to the problem highlights the importance of understanding decimal numbers. Decimals are a crucial part of our number system, allowing us to represent values that are less than one. They extend the place value system beyond the ones place, incorporating tenths, hundredths, thousandths, and so on.
Place Value in Decimal Numbers: A Closer Look
Understanding place value is key to working with decimals. Consider the number 0.7:
- 0: This is the ones place, representing zero whole units.
- . (Decimal Point): This separates the whole number part from the fractional part.
- 7: This is the tenths place, representing seven tenths (7/10).
The decimal point is a crucial element, indicating the position of each digit relative to the ones place.
Representing Decimals: Fractions and Percentages
Decimals can also be represented as fractions and percentages. In this case, 0.7 can be expressed as:
- Fraction: 7/10
- Percentage: 70%
Understanding these different representations enhances flexibility in calculations and problem-solving.
Real-World Applications of Decimal Numbers
Decimal numbers are not just abstract mathematical concepts; they are essential tools used in numerous real-world situations:
- Finance: Calculating interest rates, managing bank accounts, and understanding stock prices all rely on decimals.
- Measurement: Measuring length, weight, volume, and temperature often involves decimal numbers.
- Science: Scientific data, experimental results, and calculations frequently utilize decimals for precision.
- Technology: Computer programming, digital design, and engineering all depend heavily on the use of decimals.
- Everyday Life: Calculating tips, splitting bills, measuring ingredients in cooking, and determining fuel efficiency all involve decimal numbers.
Expanding the Concept: Similar Problems and Variations
The core principle of solving "7 is ten times the value of what number?" can be applied to various similar problems. For instance:
- 15 is five times the value of what number? (Solution: 3)
- 24 is twelve times the value of what number? (Solution: 2)
- 0.8 is ten times the value of what number? (Solution: 0.08)
By changing the numbers, we can explore different aspects of multiplication and division, strengthening our understanding of these fundamental mathematical operations.
Mastering Decimals: Practice and Resources
Consistent practice is key to mastering decimal numbers and solving related problems. Working through various examples, both simple and complex, will reinforce your understanding and build your confidence. Numerous online resources, including educational websites and interactive exercises, can provide additional practice and support.
Conclusion: From Simple Question to Deeper Understanding
The seemingly simple question, "7 is ten times the value of what number?", has led us on a journey of exploration, uncovering the importance of decimal numbers and their applications in various contexts. By understanding the underlying mathematical principles, different solution methods, and real-world applications, we have not only solved the initial problem but also broadened our mathematical understanding. This foundation will prove invaluable as we tackle more complex mathematical concepts and challenges in the future. Remember, the key is consistent practice and a willingness to explore different approaches to problem-solving. The more you work with decimals, the more intuitive and effortless they will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7 Is Ten Times The Value Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.