3 6 9 15 24 39
New Snow
May 10, 2025 · 5 min read
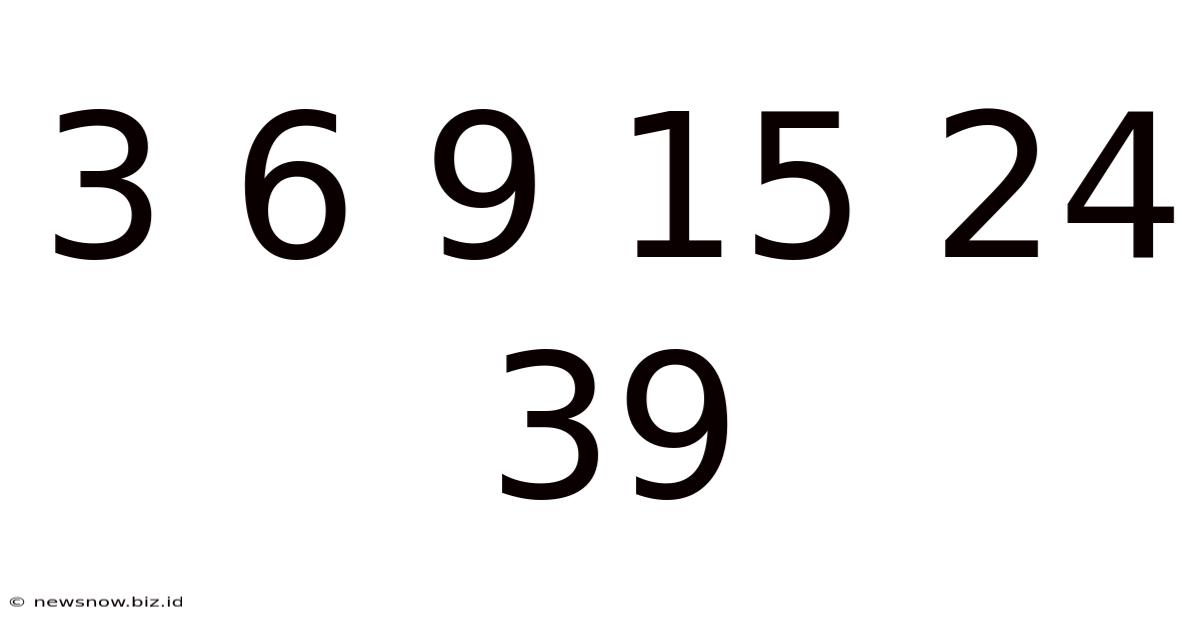
Table of Contents
Unlocking the Mysteries of the Sequence: 3, 6, 9, 15, 24, 39...
The seemingly simple sequence 3, 6, 9, 15, 24, 39… might appear innocuous at first glance. However, a deeper dive reveals a fascinating interplay of mathematical patterns and potential connections to various mathematical concepts. This article explores the different ways to interpret this sequence, uncovering the underlying logic and exploring potential extensions. We’ll examine various approaches to understanding this sequence, looking at differences, ratios, and potential underlying formulas. Our goal is to not only understand the sequence itself but also develop a methodology for approaching similar numerical puzzles.
Understanding the Differences
One of the first steps in analyzing any numerical sequence is to look at the differences between consecutive terms. This often reveals underlying patterns. Let's calculate the differences between consecutive terms in our sequence:
- 6 - 3 = 3
- 9 - 6 = 3
- 15 - 9 = 6
- 24 - 15 = 9
- 39 - 24 = 15
Notice a pattern? The differences themselves form a sequence: 3, 3, 6, 9, 15. This new sequence mirrors the original sequence's initial terms, but with a slight shift. This suggests a recursive relationship—the next difference is derived from the preceding terms in the original sequence. This recursive nature is a key characteristic that allows us to continue the sequence.
Recursive Formula
We can express this recursive relationship more formally. If we denote the nth term of the original sequence as a<sub>n</sub>, then we can represent the recursive formula as:
a<sub>n+1</sub> = a<sub>n</sub> + d<sub>n</sub>
Where d<sub>n</sub> is the nth difference, and initially, d<sub>1</sub> = 3, then d<sub>n</sub> = a<sub>n-1</sub> for n > 1.
This formula precisely describes how each subsequent term is generated. This recursive definition offers a clear method for extending the sequence infinitely.
Exploring Further Differences and Patterns
Let's take this a step further. If we look at the second differences (the differences between the differences), we find:
- 3 - 3 = 0
- 6 - 3 = 3
- 9 - 6 = 3
- 15 - 9 = 6
This sequence of second differences, 0, 3, 3, 6, shows less obvious regularity than the first difference sequence. However, we can observe a potential connection between the sequence of second differences and the original sequence. The first two elements of the second differences show a clear pattern while the next two seem to mirror the same pattern with a delay of one element.
This analysis highlights that while a simple arithmetic progression isn't directly evident, a more complex recursive relationship underlies the sequence's structure.
Beyond Differences: Examining Ratios
Instead of focusing solely on differences, let's explore the ratios between consecutive terms:
- 6 / 3 = 2
- 9 / 6 = 1.5
- 15 / 9 = 1.666...
- 24 / 15 = 1.6
- 39 / 24 = 1.625
The ratios aren't as immediately revealing as the differences. There's no consistent ratio, suggesting that this sequence doesn't follow a simple geometric progression. This lack of a consistent ratio further strengthens the indication that a more sophisticated mathematical structure underlies the pattern.
Potential Extensions and Generalizations
Based on the recursive formula we established, we can continue the sequence:
- Next difference: 24
- Next term: 39 + 24 = 63
- Next difference: 39
- Next term: 63 + 39 = 102
- Next difference: 63
- Next term: 102 + 63 = 165
And so on. The sequence continues to grow, with each term being the sum of the previous term and the term before the previous term.
Connecting to Other Mathematical Concepts
While this sequence doesn't neatly fit into established mathematical series like arithmetic or geometric progressions, it shares characteristics with other mathematical structures. For example, the recursive definition hints at connections to concepts seen in Fibonacci-like sequences, where each term depends on the preceding ones. Although it's not a true Fibonacci sequence (where each term is the sum of the two preceding terms), it exhibits a similar recursive property.
The sequence also displays elements of combinatorial mathematics, although the precise combinatorial interpretation may require further investigation. The lack of a readily apparent closed-form formula (a formula that directly calculates the nth term without calculating previous terms) further underlines its complexity.
Practical Applications and Further Research
While the primary value of this sequence lies in its mathematical curiosity, such sequences often have unexpected applications. Similar recursively defined sequences are used in various fields, including:
- Modeling growth patterns: Sequences like this can model growth processes where the rate of growth is influenced by previous growth stages.
- Computer science: Recursion is a fundamental concept in computer science, and analyzing recursive sequences like this can provide insights into algorithmic complexity.
- Financial modeling: Recursive relationships are commonly found in financial models, where future values depend on past values.
Further research could explore:
- Finding a closed-form expression: The existence of a closed-form formula that directly generates the nth term remains an open question.
- Exploring deeper connections to other mathematical structures: The relationship to Fibonacci-like sequences and combinatorial mathematics deserves further investigation.
- Analyzing the behavior of the sequence as n approaches infinity: Understanding the asymptotic growth rate of the sequence would offer valuable insights.
Conclusion
The seemingly simple sequence 3, 6, 9, 15, 24, 39… reveals a surprising depth of mathematical complexity. Through analyzing differences, ratios, and exploring its recursive nature, we've uncovered a sophisticated mathematical structure that defies easy categorization. While it doesn't fit neatly into established mathematical series, its recursive definition and potential connections to other areas of mathematics make it a fascinating object of study. The exploration of this sequence serves as a valuable example of how even simple-looking numerical patterns can reveal intriguing mathematical properties. Further research promises to unveil more of the secrets hidden within this intriguing number sequence. The methods outlined here can be applied to other sequences, providing a valuable framework for analyzing and understanding numerical patterns. The journey of uncovering the underlying structure of this sequence showcases the beauty and complexity inherent in mathematical exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 6 9 15 24 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.